Peluang (Materi Ringkasan)

Follow @HediSasrawan

1. Kaidah Pencacahan

1.1. Aturan Perkalian

Jika kejadian pertama dapat terjadi dalam m cara dan kejadian kedua dapat terjadi dalam n cara maka dua kejadian tersebut dapat terjadi bersama-sama dalam m x n cara.

Misalkan:	Peristiwa 1 dapat terjadi dalam n1 cara.
	Peristiwa 2 dapat terjadi dalam n2 cara.
	Peristiwa 3 dapat terjadi dalam n3 cara.
	……………………………………………
	Peristiwa k dapat terjadi dalam nk cara.

Banyak cara k peristiwa dapat dilaksanakan secara berurutan adalah:

n = n₁ x n₂ x n₃ x … x n_k

1.2. Faktorial

Perkalian n bilangan asli pertama disebut n faktorial, dinotasikan (dilambangkan) dengan n!.

n! = n x (n-1) x (n-2) x (x-3) x … x 3 x 2 x 1

8! = 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1

1.3. Permutasi

Permutasi adalah cara membentuk susunan terurut (urutan diperhatikan) dari sebagian atau seluruh anggota himpunan yang disediakan.

Rumus banyak permutasi:

Misalkan dalam 5 buah data akan diambil 2 data. Dengan urutan diperhatikan (misal: data 1 dan 2 berbeda dengan data 2 dan 1), berapa cara yang dapat dilakukan untuk mengambil 2 data tersebut?

Jawab:

1.4. Permutasi yang Memuat Beberapa Unsur yang Sama

Misalkan terdapat angka 6, 6, 6, 7, 7, 8, dan 9. Angka tersebut akan dibentuk beberapa bilangan yang terdiri dari 7 angka. Berapa bilangan yang dapat dibentuk?

Jawab:

Terdapat 3 angka 6

Terdapat 2 angka 7

Terdapat 1 angka 8

Terdapat 1 angka 9

n
	= 7

1.5. Permutasi Siklis

Permutasi siklis adalah susunan terurut unsur-unsur yang membentuk lingkaran (kurva tertutup). Rumus banyak permutasi siklis dari n unsur adalah:

1.6. Kombinasi

Kombinasi adalah cara membentuk susunan (urutan tidak diperhatikan) dari sebagian atau seluruh anggota himpunan yang disediakan.

Rumus banyak kombinasi:

Misalkan dalam 5 buah data akan diambil 2 data. Dengan urutan tidak diperhatikan (misal: data 1 dan 2 sama dengan data 2 dan 1), berapa cara yang dapat dilakukan untuk mengambil 2 data tersebut?

Jawab:

2. Peluang Suatu Kejadian

2.1. Menentukan Peluang Kejadian

Rumus menentukan peluang kejadian dengan pendekatan frekuensi relatif:

Rumus menentukan peluang kejadian menggunakan ruang sampel:

Keterangan:

P(A)	= peluang kejadian A
n(A)	= banyak anggota himpunan kejadian A
n(S)	= banyak anggota himpunan ruang sampel S

Rumus menentukan peluang komplemen (yang bukan) suatu kejadian:

2.2. Frekuensi Harapan

Frekuensi harapan kejadian A adalah banyaknya kejadian A yang diharapkan terjadi dalam beberapa kali percobaan dengan rumus:

Keterangan:

	= frekuensi harapan kejadian A
n	= banyak percobaan
P(A)	= peluang kejadian A

3. Peluang Kejadian Majemuk

3.1. Peluang Gabungan Dua Kejadian

Peluang gabungan dua kejadian (kejadian A atau kejadian B) ditulis ditentukan dengan rumus berikut:

Keterangan: S adalah ruang sampel.

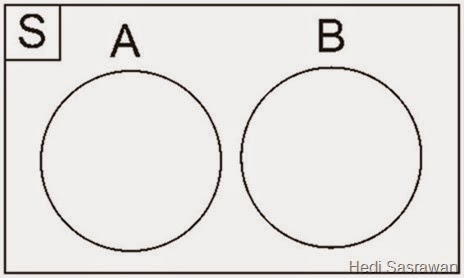
3.2. Peluang Gabungan Dua Kejadian Saling Asing

Rumus peluang gabungan dua kejadian yang saling asing adalah:

3.3. Peluang Kejadian Saling Bebas

Kejadian A dan kejadian B disebut dua kejadian yang saling bebas jika kejadian A tidak terpengaruh oleh kejadian B atau sebaliknya. Jika kejadian A dan kejadian B saling bebas, berlaku rumus:

3.4. Peluang Dua Kejadian Bersyarat

Kejadian A dan kejadian B disebut dua kejadian yang saling bersyarat jika kejadian A bergantung pada kejadian B atau sebaliknya.

Peluang kejadian A dengan syarat kejadian B terjadi lebih dahulu ditentukan dengan rumus:

Peluang kejadian B dengan syarat kejadian A terjadi lebih dahulu ditentukan dengan rumus:

---

Anda bisa request artikel tentang apa saja, kirimkan request Anda ke hedisasrawan@gmail.com